晶体管的频率响应

频率响应概述

• 电容和电感对频率的影响

$$Z_C=\frac{1}{jwc}=\frac{1}{j2\pi fc}$$

$$Z_L=jwl=j2\pi fl$$

• 频段分类

图1.1 频段分类

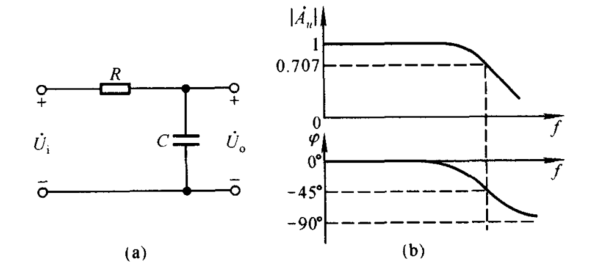
​ 上图分别为：低通、高通、带通

​ fH为上限截止频率，下降到中频增益的0.707倍时的频率

​ fL为下限截止频率，下降到中频增益的0.707倍时的频率

​ 截止频率又被称为：-3dB带宽(原因见上述公式)

$$|\dot{A}{|}_{f=f_H}(dB)=20\times lg{A}_m\frac{1}{\sqrt{2}}(dB)=20\times lg{A}_m-3.01(dB)$$

阻容基本单元的频率响应

低通单元

• 基本低通单元

图2.1 低通单元

$${\dot{A}}_u=\frac{\frac{1}{jwc}}{R+\frac{1}{jwc}}=\frac{1}{1+jwRC}=|{\dot{A}}_u|\mathrm{\angle }\phi$$

令：$w_0$ = 1/(RC)

公式补充：

​

相量法基础：

按照第一小节，的截止频率的定义可知，增益应该降为中频的0.707倍，既f = $f_0$,得

$$f_H=\frac{1}{2\pi RC}$$

• 低通变形

推广结论为：在一个电压源阻容串联回路中，如果从以任何一个电容两端电压为输出，那么它一定是一个低通电路，其上限截止频率为$\frac{1}{2\pi RC}$，其中 R 为回路中所有电阻之和，C 为回路中所有电容的串联值（类似于电阻并联计算）。

高通单元

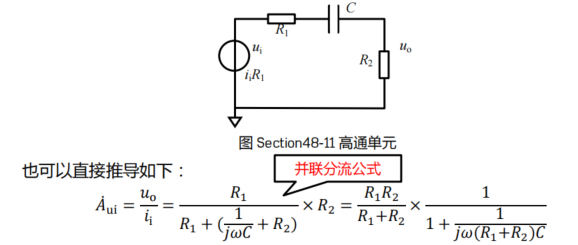
• 基本高通单元

图2.1 高通单元

$${\dot{A}}_u=\frac{R}{R+\frac{1}{jwc}}=\frac{1}{1+\frac{1}{jwRC}}=\frac{1}{1-j\frac{f_0}{f}}$$

对于最后一个图，可使用戴维林等效进行求解：

高通低通的两极判断法

​ 两极判断法，可以较为轻松的实现上述判断，方法是：

​ 第一个极，是 0Hz。此时电容容抗无穷大，在图中可以将其断开，此时求解电路增益，称为 A0；第二个极，是频率无穷大，电容容抗为 0，在图中可以将其短路，求解此时的增益，称为 A∞，然后按照下述规则判断：

​ 1）如果 A0为有限值，A∞为 0，则一定是低通，Am=A0；

​ 2）如果 A∞为有限值，A0为 0，则一定是高通，Am=A∞；

​ 3）除此之外，什么都不是：既不是高通，也不是低通。

基本单元串联的频率响应

有以下公式成立：

$$f_{H0}\approx min(f_{H1},f_{H2},f_{H3})$$

$$f_{L0}\approx max(f_{L1},f_{L2},f_{L3})$$

但是当上限截止频率相差不大，或者干脆三个值相等，则情况会变得复杂。可以直接参考下列公式进行计算

举例：
​ 高通模块(Am1=0.5，fL1=50Hz)，高通模块(Am2=2，fL1=160Hz)，低通模块(Am3=5，fH1=10000Hz)，低通模块(Am4=4，fH2=10000Hz)，低通模块(Am5=1，fH3=10000Hz)，将它们串联，求串联后的中频增益和截止频率。

• 增益

$$A_m=A_{m1}\times A_{m2}\times A_{m3}\times A_{m4}\times A_{m5}=20$$

• 高通模块

​ 只有两个，一个 50Hz，一个 160Hz，无法界定 K 值，因此：

$$\sqrt{f_{L1}^2+f_{L2}^2}=167.63Hz<f_{L0}<1.099\sqrt{f_{L1}^2+f_{L2}^2}=184.23Hz$$

• 低通模块(k=1.133)
  $$f_{H0}=\frac{1}{k\sqrt{\frac{1}{f_{H1}^2}+\frac{1}{f_{H1}^2}+\frac{1}{f_{H1}^2}+\dots \dots }}=5095.8Hz$$

晶体管放大电路的非杂散频率响应

• 放大电路分析频率响应的原因（电容）

图4.1 晶体管外部和内部的高频等效模型（含杂散）

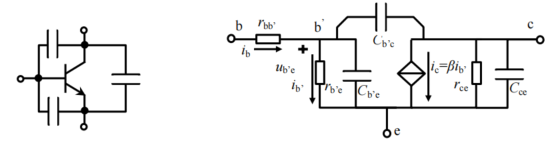
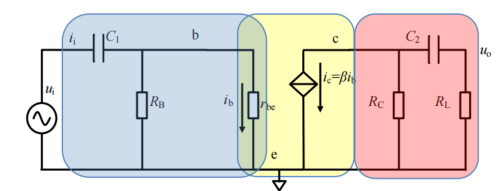
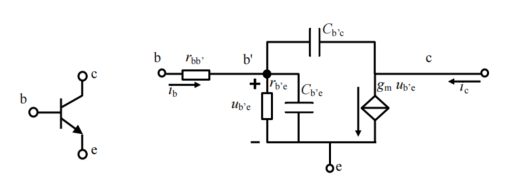
​ 首先，晶体管内部高频模型中（见图 4.1），存在 3 个结电容，它们的存在会降低放大电路的增益；其次，任何两个导体节点之间，也存在杂散电容。这些都会导致整个放大电路，在面对高频信号输入时，呈现放大倍数的逐渐下降，产生了上限截止频率

​ 因此，影响放大电路下限截止频率的关键，是电路中的隔直电容；影响晶体管放大电路上限截止频率的关键，是电路中的旁路电容，如果没有旁路电容，则要看晶体管的高频等效模型。

• 隔直电容和旁路电容

  ​ 首先二者是不会同时出现在分析电路里的。，通常在分析下限截止频率时，只考虑隔直电容，而将旁路电容视为开路。而在分析上限截止频率时，只考虑旁路电容，而将隔直电容视为短路。

  ​ 隔直电容通常比旁路电路大得多，因此在相同信号频率下，隔直电容的容抗要远小于旁路电容之容抗，如下图所示：

  

  例如：在正常的音频放大器中，考虑到人耳敏感的频段在 20Hz~20kHz，一般会设计成下限截止频率为 1Hz~10Hz，而上限

  截止频率一般为 100kHz 左右。这样可以保证在 20Hz~20kHz 之间，放大器具有较为平坦的幅频特性。

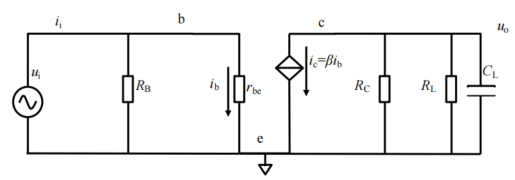
  ​ 比如 10Hz 附近时，电路中的 C1和 C2表现出明显非 0 的容抗，约为 1592Ω，会明显降低电路的放大倍数。而此时容值很小的 CL（一般为 1nF 数量级）的容抗约为 15.9MΩ，它并联在负载电阻上，几乎不会引起输出幅度的改变。即，研究有 C1 和 C2 引起的下限截止频率时，无需考虑 CL 的存在，可将其视为开路。

  ​ 同样，当我们关心 100kHz 附近的上限截止频率时，CL 的容抗约为 1592Ω，并联于负载电阻上，以及足以引起输出幅度的下降。而此时，C1 和 C2 的容抗非常小，约为 0.159Ω，完全可以忽略，则可将其视为短路。

• 下限截止频率求解

  

  图4.2 含电容的低频段动态等效电路
  $$\begin{array}{}{\dot{A}}_o=\frac{{\dot{u}}_o}{u_i}=\frac{{\dot{i}}_b}{u_i}\times \frac{{\dot{i}}_c}{{\dot{i}}_b}\times \frac{{\dot{u}}_o}{{\dot{i}}_c}={\dot{A}}_1\times {\dot{A}}_2\times {\dot{A}}_3\\ {\dot{A}}_1=\frac{{\dot{i}}_b}{u_i}=\frac{u_i\frac{R}{R+\frac{1}{j\omega C_1}}\times \frac{1}{r_{b}e}}{u_i}=\frac{1}{r_{b}e}\times \frac{1}{1+\frac{1}{j\omega R{C}_1}}\\ A_{m1}=\frac{1}{r_{b}e},f_{L1}=\frac{1}{j\omega (R_B//r_{be})C_1}\\ \mathrm{对}{\dot{A}}_2\mathrm{来}\mathrm{说}，\mathrm{就}\mathrm{是}\mathrm{一}\mathrm{个}\mathrm{电}\mathrm{流}\mathrm{放}\mathrm{大}\mathrm{器}\beta ，\mathrm{它}\mathrm{不}\mathrm{受}\mathrm{频}\mathrm{率}\mathrm{影}\mathrm{响}，\mathrm{因}\mathrm{此}\mathrm{下}\mathrm{限}\mathrm{截}\mathrm{止}\mathrm{频}\mathrm{率}\mathrm{为}0。\mathrm{本}\mathrm{级}\mathrm{对}\mathrm{整}\mathrm{个}\mathrm{放}\mathrm{大}\mathrm{电}\mathrm{路}\mathrm{的}\mathrm{下}\mathrm{限}\mathrm{截}\mathrm{止}\mathrm{频}\mathrm{率}\mathrm{没}\mathrm{有}\mathrm{影}\mathrm{响}\\ A_{m2}=\beta ,f_{L2}=0\\ \mathrm{对}{\dot{A}}_3\mathrm{来}\mathrm{说}，\mathrm{是}\mathrm{基}\mathrm{本}\mathrm{高}\mathrm{通}\mathrm{的}\mathrm{一}\mathrm{个}\mathrm{变}\mathrm{形}，\mathrm{可}\mathrm{参}\mathrm{考}\mathrm{基}\mathrm{本}\mathrm{高}\mathrm{通}（\mathrm{戴}\mathrm{维}\mathrm{林}\mathrm{等}\mathrm{效}）\\ {\dot{A}}_3=\frac{{\dot{u}}_o}{{\dot{i}}_c}=\frac{R_C{R}_L}{R_C+R_L}\times \frac{1}{1+\frac{1}{j\omega (R_L+R_C)C_2}}\\ A_{m3}=\frac{R_C{R}_L}{R_C+R_L},f_{L3}=\frac{1}{2\pi (R_L+R_C)C_2}\end{array}$$

  其中：$R=R_B//r_{be}$,跨导放大器。结合上一小节的公式，就能求解

• 上限截止频率求解

  

  图4.3 含电容的高频段动态等效电路
  $$\begin{array}{}{\dot{A}}_1=\frac{1}{r_{be}}\\ {\dot{A}}_2=\beta \\ {\dot{A}}_3=R_C//R_L//\frac{1}{j\omega C_L}\\ \mathrm{只}\mathrm{有}\mathrm{第}\mathrm{三}\mathrm{个}\mathrm{环}\mathrm{节}\mathrm{具}\mathrm{有}\mathrm{上}\mathrm{限}\mathrm{截}\mathrm{止}\mathrm{频}\mathrm{率}（\mathrm{戴}\mathrm{维}\mathrm{林}\mathrm{等}\mathrm{效}）\\ f_H=\frac{1}{2\pi (R_C//R_L)C_L}\end{array}$$

举例：

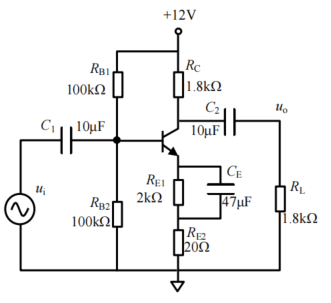
晶体管 β=100，rbb’=10Ω，UBEQ=0.7V。求解电路的下限截止频率。当负载并接 CL=6.8nF 电容，求解电路的上限截止频率。

• 电路化简

1.去掉基极偏置电阻 RB1 和 RB2，它们和基极电阻相比实在太大了，对 ib 的分流影响微乎其微

2.去掉发射极电阻 RE1。

​ 对上述电路进行静态分析（不熟悉，回顾晶体管基础对应部分）：rbe = 1256Ω，晶体管处于放大状态

​ Re1影响输入电流Ib。

​ 分析过程为：从中频段开始，降到增益的0.707倍结束。

​ 中频段输入的电阻为$r=r_{be}+(1+\beta )R_{E2}=3276\Omega$， 当阻抗变为此时的1.414倍时（此时Ib减小到0.707倍），有

$$|\dot{Z}|=|\frac{1}{j\omega C_1}+r_{be}+(1+\beta )(R_{E2}+R_{E1}//\frac{1}{j\omega C_E})|=\sqrt{2}\times 3276$$

​ 可以看到RE几乎一点作用都不起（$R_{E1}//\frac{1}{j\omega C_E})=30.54$,基本上是由CE的容抗变化也引起的），

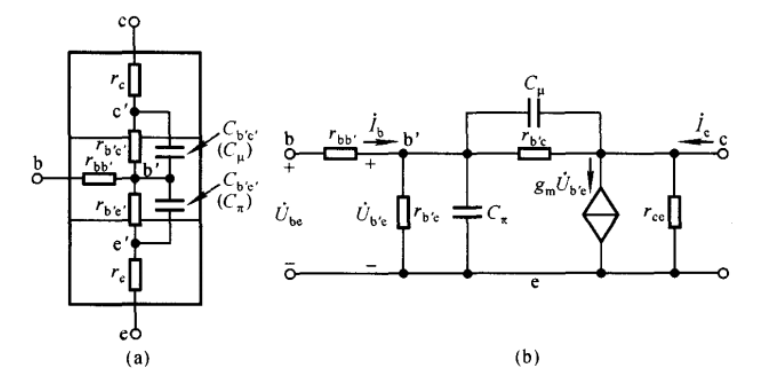
晶体管高频等效模型

以𝑟b′e两端的电压𝑢b′e控制输出受控源，因此输出受控源的表达式变为：${𝑔}_{𝑚}{U}_{b^{\prime }e}$。其中：

$$g_m=\frac{\beta }{r_{b^{\prime }e}}$$

上图所示图形中，rb’c集电结电容，通常200k到500k。所以通常简化图形如下

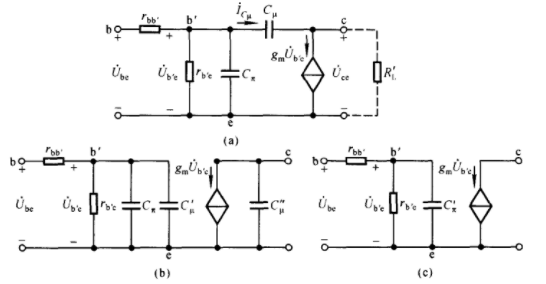
密勒等效：

​ 分析流程可自行计算（利用分离前后电流依旧相等进行计算）

​ 密勒电容：跨接在输入端和输出端之间的电容

​ 结论：该电容反应到输入端，放大1+A倍。

密勒电容可以使得电路的低频特性大大降低（密勒），相当于输入电路（低通）的电容被放大了，f自然就减小了

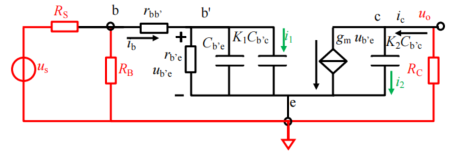
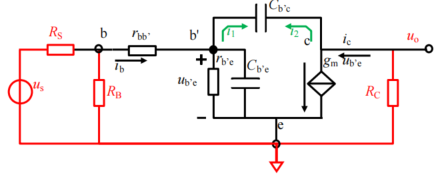
高频分析方法：

​ 根据上述的密勒效应，明显$C_{\mu }$就是密勒电容。

​ （C图中因为电容的容抗，一般远远大于RL，所以流过的电流也可以忽略不计）

关键参数计算：

• $$r_{b^{\prime }e}$$
  $$r_{b^{\prime }e}=(1+\beta )\frac{U_T}{I_{EQ}}$$
• $$g_m$$
  $$g_m=\frac{\beta }{r_{b^{\prime }e}}$$
• $$C_{\pi }^{\prime }$$
  $$C_{\pi }^{\prime }=C_{\pi }+C_{\mu }"$$

共射放大电路的频率响应

• k1求解

  等效前的电路：

  

  根据密勒等效：

  $$A=\frac{U_c}{U_{b^{\prime }}}=\frac{g_m{U}_{b^{\prime }e}{R}_c}{U_{b^{\prime }e}}=g_m{R}_c$$
  $$\begin{array}{}k1=1+A\\ k2=1\end{array}$$

• 截止频率